Краткая теория
Понятие очереди всем хорошо известно из повседневной жизни. Элементами очереди в общем случае являются заказы на то или иное обслуживание: выбить чек на нужную сумму в кассе магазина, получить нужную информацию в справочном бюро, выполнить очередную операцию по обработке детали на данном станке в автоматической линии и т.д.
В программировании имеется структура данных, которая называется очередь. Эта структура данных используется, например, для моделирования реальных очередей с целью определения их характеристик (средняя длина очереди, время пребывания заказа в очереди и т.п.) при данном законе поступления заказов и дисциплине их обслуживания.
По своему существу очередь является полустатической структурой - с течением времени и длина очереди, и набор образующих ее элементов могут изменяться.
Различают два основных вида очередей, отличающихся по дисциплине обслуживания находящихся в них элементов :
1. При первой из дисциплин заказ, поступивший в очередь первым, выбирается первым для обслуживания (и удаляется из очереди). Эту дисциплину обслуживания принято называть FIFO (First input-First output, т.е. первый пришел - первый ушел). Очередь открыта с обеих сторон.

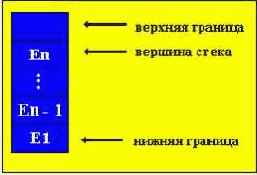
2. Вторую дисциплину принято называть LIFO (Last input - First output, т.е. последний пришел - первый ушел), при которой на обслуживание первым выбирается тот элемент очереди, который поступил в нее последним. Очередь такого вида в программировании принято называть СТЕКОМ (магазином) - это одна из наиболее употребительных структур данных, которая оказывается весьма удобной при решении различных задач.
В силу указанной дисциплины обслуживания, в стеке доступна единственная его позиция, которая называется ВЕРШИНОЙ стека - эта позиция, в которой находится последний по времени поступления в стек элемент. Когда мы заносим новый элемент в стек, то он помещается поверх вершины и теперь уже сам находится в вершине стека. Выбрать элемент можно только из вершины стека; при этом выбранный элемент исключается из стека, а в его вершине оказывается элемент, который был занесен в стек перед выбранным из него элементом (структура с ограниченным доступом к данным).
До сих пор мы рассматривали только статические программные объекты. Этим термином обозначаются объекты, которые порождаются непосредственно перед выполнением программы, существуют в течение всего времени ее выполнения и размер значений которых не изменяется по ходу выполнения программы.
Поскольку статические объекты порождаются до выполнения программы и размер их значений можно выделить еще на этапе трансляции исходного текста программы на языке машины.
Однако использование при программировании только статических объектов может вызвать определенные трудности, особенно с точки зрения получения эффективной машинной программы, а такая эффективность бывает чрезвычайно важной при решении ряда задач. Дело в том, что иногда мы заранее не знаем не только размера значения того или иного программного объекта, но даже и того, будет существовать этот объект или нет. Такого рода программные объекты , которые возникают уже в процессе выполнения программы, называют динамическими объектами.
В языке ПАСКАЛЬ для работы с динамическими объектами предусматривается специальный тип данных - так называемый ссылочный тип. Значением этого типа является ссылка на какой - либо программный объект, по которой осуществляется непосредственный доступ к этому объекту. На машинном языке такая ссылка как раз и представляется указанием места в памяти соответствующего объекта.
В этом случае для описания действий над динамическими объектами каждому такому объекту в программе сопоставляется статическая переменная ссылочного типа - в терминах этих ссылочных переменных и описываются действия над соответствующими динамическими объектами.
Итак, динамические структуры данных имеют две особенности :
1. Заранее не определимо количество элементов в структуре;
2. Элементы динамической структуры не имеют жесткой линейной упорядоченности. Они могут быть разбросаны по памяти.
Чтобы связать элементы динамической структуры между собой, в состав элемента помимо информационного поля входят поля указателей (связок с другими элементами структуры) .
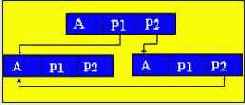
p1, p2 - указатели, содержащие адреса элементов, с которыми данный элемент связан.
Наиболее распространенными динамическими структурами являются связанные списки. С точки зрения логического представления различают линейные и нелинейные списки. В линейных списках связи строго упорядочены. Указатель предыдущего элемента дает адрес последующего элемента или наоборот.
К линейным спискам относятся односвязные и двусвязные списки.
К нелинейным - многосвязные списки.
Элемент списка в общем случае представляет собой комбинацию поля записи (информационного поля) и одного или нескольких указателей.
О том, что из себя представляют списки говорилось в предыдущей работе. Мы рассматривали однонаправленные списки, теперь мы рассмотрим кольцевые списки.

Как видно на рисунке, список замыкается в своеобразное "кольцо": двигаясь по ссылкам, можно от последнего элемента списка переходить к заглавному элементу. В связи с этим списки подобного рода называют кольцевыми списками.
Чтобы закольцевать список необходимо присвоить указателю последнего элемента указатель начала списка (Ptr(p)=lst).
Ptr(p) - указатель последнего элемента;
Lst - указатель начала списка.
Формулировка задачи.
Пусть обслуживающая система состоит из конечного числа обслуживающих аппаратов. Система относится к числу систем с ожиданием. Каждый аппарат может обслуживать одновременно только одно требование. Если в момент поступления очередного требования имеются свободные аппараты, то один из них немедленно приступает к обслуживанию, если свободных аппаратов нет, то требование ждет обслуживания. Естественно, если требований больше, чем обслуживающих аппаратов, то образуется очередь. Время обслуживания одного требования есть случайная величина, подчиненная показательному закону распределения:
F(t)=1-e-nt
Поток поступающих требований ограничен, то есть одновременно в системе обслуживания не может находиться больше m требований, где m - конечное число. Это дает право считать, что требования на обслуживание поступают от m обслуживаемых объектов, которые время от времени нуждаются в обслуживании. Пусть вероятность того, что поступит заявка на обслуживания на данном такте равна Р(А) и вероятность того, что требование из очереди поступит на обслуживание равно Р(В) ( на каждом такте может поступить не более одной заявки на обслуживание). Число обслуживающих аппаратов равно N. Допустим, требование дождалось своей очереди и оно начало обслуживаться. Обслуживание может длиться в течении не более 3-х тактов. Заявки могут быть двух приоритетов:
Заявка первого приоритета:
Это обычная заявка, она не обладает ни какими привилегиями. Она может покинуть систему через определенное число тактов Т. При приходе в обслуживающую систему заявка первого приоритета становится в конец очереди.
Заявка второго приоритета:
Эта заявка отличается только тем, что она при поступлении в обслуживающую систему становится в начало очереди, то есть как только освобождается аппарат, то она поступает на обслуживание с вероятностью Р(В).
Заявка второго приоритета , как и заявка первого приоритета, покидает систему через Т тактов. Естественно, что появление заявок второго приоритета достаточно мало ( хотя эта вероятность задается пользователем и может быть любой ). Теперь об обслуживании: Количество тактов, в течение которых будет обслуживаться та или иная заявка выбирается случайно (эта величина в данной задаче не должна быть больше 3). Если заявка обслужилась положенное ей число тактов, то она покидает систему. Если заявка находится в очереди больше Т тактов, то она с некоторой вероятностью покидает систему.
Общие сведения о структуре данных – дерево.
Дерево - это нелинейная связанная структура данных, характеризуемая следующими признаками :
- дерево имеет один элемент, на который нет ссылок от других элементов. Этот элемент, или "узел", называется корнем дерева;
- в дереве можно обратиться к любому элементу путем прохождения конечного числа ссылок (указателей) ;
- каждый элемент дерева связан только с одним предыдущим элементом.
- внутренняя сортировка - это сортировка, происходящая в оперативной памяти машины
- внешняя сортировка - сортировка во внешней памяти.
Каждый узел дерева может быть промежуточным (элементы 2,3,5,7) либо терминальным ("листом" дерева) (элементы 4,9,10,11,8,6). Характерной особенностью терминальных узлов является отсутствие ветвей.
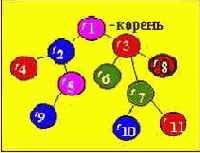
Элемент Y, находящийся непосредственно ниже элемента X, называется непосредственным потомком X, если X находится на уровне i , то говорят, что Y лежит на уровне i+1.
Считается, что корень лежит на уровне 0.
Число непосредственных потомков элемента называется его степенью исхода, в зависимости от степени исхода узлов деревья классифицируют :
A) Если степень исхода узлов - М, то дерево называется М-арным ;
B) Если степень исхода узлов - М или 0, то - полное М-арное дерево;
C) Если степень исхода узлов дерева равна 2, то дерево называется бинарным ;
D) Если степень исхода равна 2 или 0, то - полное бинарное дерево.
Особенно важную роль играют бинарные деревья, далее мы будем рассматривать их более подробно.
Представление деревьев в памяти ЭВМ
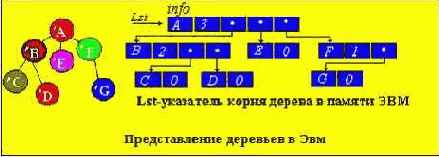
Деревья наиболее удобно представлять в памяти ЭВМ в виде связанных нелинейных списков. Элемент должен содержать INFO-поле, где содержится характеристика узла. Следующее поле определяет степень исхода узла и количество полей указателей равное степени исхода. Каждый указатель элемента ориентирует данный элемент-узел с его сыновьями. Узлы, в которые входят стрелки от исходного элемента, называются его сыновьями.
INFO-поле содержит два поля : поле записи (rec) и поле ключа (key). Ключ задается числом, по ключу определяют место элемента в дереве.
Сведение М-арного дерева к бинарному
При обработке данных в ЭВМ важно знать и информационное поле элемента, и его размещение в памяти машины. Для этих целей используется сортировка. Итак, сортировка- -это расположение данных в памяти в регулярном виде по их ключам. Регулярность рассматривают как возрастание значения ключа от начала к концу в массиве.
Различают следующие типы сортировок:
§ внутренняя сортировка - это сортировка, происходящая в оперативной памяти машины
§ внешняя сортировка - сортировка во внешней памяти.
Если сортируемые записи занимают большой объем памяти, то их перемещение требует больших затрат. Для того, чтобы их уменьшить, сортировку производят в таблице адресов ключей, делают перестановку указателей, т.е. сам массив не перемещается. Это метод сортировки таблицы адресов.
При сортировке могут встретиться одинаковые ключи. В этом случае при сортировке желательно расположить после сортировки одинаковые ключи в том же расположении, что и в исходном файле. Это устойчивая сортировка.
Эффективность сортировки можно рассмотреть с нескольких критериев:
§ время, затрачиваемое на сортировку
§ объем оперативной памяти, требуемой для сортировки
§ время, затраченное программистом на написание программы
Рассмотрим второй критерий подробнее: мы можем подсчитать количество сравнений при выполнении сортировки или количество перемещений.
Предположим, что число сравнений определяется формулой:
C = 0,01n2 + 10n
Если n<1000, то второе слагаемое больше.
Если n>1000, то первое слагаемое больше.
То есть, при малых n порядок сравнения равен , а при больших n он равен n.
Различают следующие методы сортировки:
§ строгие (прямые) методы
§ улучшенные методы
Рассмотрим преимущества прямых методов:
1.
В общем сортировку следует понимать как процесс перегруппировки заданного множества объектов в некотором определенном порядке. Цель сортировки облегчить последующий поиск элементов в таком отсортированном множестве. Это почти универсальная, фундаментальная деятельность. Мы встречаемся с отсортированными объектами в телефонных книгах, в списках подоходных налогов, в оглавлениях книг, в библиотеках, в словарях, на складах почти везде, где нужно искать хранимые объекты. Даже малышей учат держать свои вещи "в порядке", и они уже сталкиваются с некоторыми видами сортировок задолго до того, как познакомятся с азами арифметики.
Таким образом, разговор о сортировке вполне уместен и важен, если речь идет об обработке данных. Что может легче сортироваться, чем данные? Тем не менее наш первоначальный интерес к сортировке основывается на том, что при построении алгоритмов мы сталкиваемся со многими весьма фундаментальными приемами. Почти не существует методов, с которыми не приходится встречаться при обсуждении этой задачи. В частности, сортировка это идеальный объект для демонстрации огромного разнообразия алгоритмов, все они изобретены для одной и той же задачи, многие в некотором смысле оптимальны, большинство имеет свои достоинства. Поэтому это еще и идеальный объект, демонстрирующий необходимость анализа производительности алгоритмов. К тому же на примерах сортировок можно показать, как путем усложнения алгоритма, хотя под рукой и есть уже очевидные методы, можно добиться значительного выигрыша в эффективности.
Выбор алгоритма зависит от структуры обрабатываемых данных это почти закон, но в случае сортировки такая зависимость столь глубока, что соответствующие методы были даже разбиты на два класса сортировку массивов и сортировку файлов последовательностей . Иногда их называют внутренней и внешней сортировкой, поскольку массивы хранятся в быстрой оперативной, внутренней памяти машины со случайным доступом, а файлы обычно размещаются в более медленной, но и более емкой внешней памяти, на устройствах, основанных на механических перемещениях дисках или лентах .
Пузырьковая сортировка
Идея : (N-1) раз массив проходится снизу вверх (сверху вниз), при этом элементы попарно сравниваются, если нижний элемент меньше верхнего, то элементы переставляются.
Пример : массив - 4, 3, 7, 2, 1, 6.
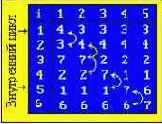
Можно улучшить "пузырьковый" метод, если проходить массив элементов и вверх и вниз одновременно.
Количество сравнений :

Количество перемещений :

Пример вычисления "пузырьковым" методом
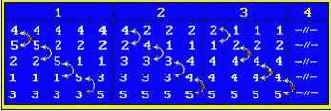
На примере представлен массив из пяти элементов, это означает, что массив проходится снизу вверх (сверху вниз) 5-1=4 раза. Так же на примере видно, что алгоритм "в пустую" обрабатывает массив начиная уже с третьего шага внутреннего цикла, а 4-й шаг можно уже не выполнять.
Преимущества данного метода :
1) Самый простой алгоритм
2) Простой в реализации
3) Не нужно дополнительных переменных
Недостатки:
1) Долго обрабатывает большие массивы
2) В любом случае количество проходов не уменьшается
Quiksort - метод быстрой сортировки
Идея : В основе данного метода положен метод разделение ключей по отношению к выбранному.
Пример :
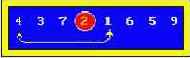
После первого прохода выбранный элемент становится на свое место.
Улучшение "пузырькового" метода.
1) Если проходить массив не только сверху вниз, но и снизу вверх одновременно, то не только "легкие" элементы будут "всплывать", но и "тяжелые" "тонуть".
2) Для отмены прохода массива "впустую" нужно в во внешний цикл вставить проверку на отсортированность массива.
При обработке данных в ЭВМ важно знать и информационное поле элемента, и его размещение в памяти машины. Для этих целей используется сортировка. Итак, сортировка - это расположение данных в памяти в регулярном виде по их ключам. Регулярность рассматривают как возрастание значения ключа от начала к концу в массиве.
Различают следующие типы сортировок:
Схематичное представление двоичного дерева : имеется набор вершин, соединенных стрелками. Из каждой вершины выходит не более двух стрелок (ветвей ), направленных влево - вниз или вправо - вниз. Должна существовать единственная вершина, в которую не входит ни одна стрелка - эта вершина называется корнем дерева. В каждую из оставшихся вершин входит одна стрелка.
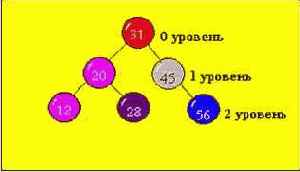
Существует множество способов упорядочивания дерева. Рассмотрим один из них :
" Левый " сын имеет ключ меньше, чем ключ " Отца "
" Правый " сын имеет ключ больше, чем ключ " Отца "
Получили бинарное упорядоченное дерево с минимальным числом уровней.
Строго сбалансированное дерево : дерево, в котором левое и правое поддерево имеют уровни , отличающиеся не более, чем на единицу.
Рассмотрим принцип построения дерева при занесении элементов в массив :
Пусть в первоначально пустой массив заносятся последовательно поступающие элементы : 70, 60, 85, 87, 90, 45, 30, 88, 35, 20, 86 ; Т.к. это еще пустое дерево, то ссылки left и right равны nil( left - указатель на левого сына (элемент), right - указатель на правого сына (элемент)).
Четвертый из поступающих элементов 87. Т.к. этот ключ больше ключа 70 ( корень ), то новая вершина должна размещаться на правой ветви дерева. Чтобы определить ее место, спускаемся по правой стрелке к очередной вершине ( с ключом 85 ), и если поступивший ключ больше 85, то новую вершину делаем правым сыном вершины с ключом 85 .
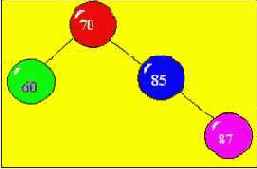
В рассмотренном примере ПРИНЦИП ПОСТРОЕНИЯ ДЕРЕВА имеет следующий вид : если поступает очередной элемент массива, то начиная с корня дерева (в зависимости от сравнения текущего элемента с очередной вершиной) идем влево или вправо от нее до тех пор, пока не найдем подходящую вершину, к которой можно подключить новую вершину с текущим ключом. В зависимости от результата сравнения ключей, новую вершину делаем левой или правой для найденной вершины.
ПОИСК
Одно из наиболее часто встречающихся в программировании действий - поиск. Он же представляет собой идеальную задачу, на которой можно испытывать различные структуры данных по мере их появления. Существует несколько основных "вариаций этой темы", и для них создано много различных алгоритмов. При дальнейшем рассмотрении мы исходим из такого принципиального допущения: группа данных, в которой необходимо отыскать заданный элемент, фиксирована. Будем считать, что множество из N элементов задано, скажем, в виде такого массива
a: ARRAY[0..N-1] OF item
Обычно тип item описывает запись с некоторым полем, выполняющим роль ключа. Задача заключается в поиске элемента, ключ которого равен заданному "аргументу поиска" x. Полученный в результате индекс i, удовлетворяющий условию a[i].key=x, обеспечивает доступ к другим полям обнаруженного элемента. Так как нас интересует в первую очередь сам процесс поиска, а не обнаруженные данные, то мы будем считать, что тип item включает только ключ, т.е. он есть ключ (key).
ПОИСК (SEARCH) является одной из основ обработки данных в ЭВМ. Его назначение состоит в том, чтобы по заданному аргументу найти среди массива данных те данные, которые соответствуют этому аргументу или определить, что этих данных нет. Если этих данных нет, добавить их в массив данных.
Набор любых данных будем называть ТАБЛИЦЕЙ или ФАЙЛОМ. Данное или элемент структуры отличается каким-то признаком от других данных. Этот признак называется КЛЮЧОМ. Ключ может быть УНИКАЛЬНЫМ, т.е. в таблице только одно данное с таким ключом, иначе уникальные ключи называются ПЕРВИЧНЫМИ КЛЮЧАМИ.
ВТОРИЧНЫЙ КЛЮЧ в одной таблице может повторяться, но по нему тоже можно организовать поиск. Ключи данных собраны в одном месте (таблице).
Ключи, которые выделены из таблицы данных и организованы в свой файл, называются ВНЕШНИМИ КЛЮЧАМИ. Если ключ в записи, то он называется ВНУТРЕННИМ КЛЮЧОМ.
ПОИСКОМ ПО ЗАДАННОМУ АРГУМЕНТУ называется алгоритм, определяющий соответствие ключа данного с заданным аргументом. Результатом работы алгоритма поиска может быть нахождение этого данного или отсутствие данного в таблице. В случае отсутствия данного возможны две операции:
1. Индикация того, что данного нет.
2. Вставка данного в таблицу.
Пусть К - массив ключей, тогда для всех К(i) существует R(i) - данное. KEY - аргумент поиска. Ему соответствует информационная запись REC. В зависимости от того, какова структура данных в таблице, различают несколько видов поиска.
ПЕРЕУПОРЯДОЧЕНИЕ ТАБЛИЦЫ ПОИСКА
Всегда можно говорить о некотором значении вероятности нахождения того или иного элемента.
P(i) - вероятность нахождения элемента.
В этом случае таблица поиска представляется как система с дискретными состояниями, а искомый элемент характеризуется i-ым состоянием системы, вероятность которого P(i).
P(1) + P(2) + ... + P(n) = 1
Количество сравнений Z при поиске в таблице, т.е. количество сравнений, необходимых для поиска по заданному аргументу, представляет собой значение дискретной случайной величины, определяемой номерами состояний и вероятностями состояний системы.
Z=1*P(1) + 2*P(2) + 3*P(3) + ... + n*P(n)
ТАБЛИЦА ДАННЫХ ДОЛЖНА БЫТЬ УПОРЯДОЧЕНА ТАКИМ ОБРАЗОМ , чтобы в начале таблицы были элементы с большими вероятностями поиска или элементы , к которым чаще всего обращаются в таблице.
P(1) >= P(2) >= P(3) >= ... >= P(n)
ИМЕЕТСЯ ДВА ОСНОВНЫХ МЕТОДА ПЕРЕУПОРЯДОЧЕНИЯ ТАБЛИЦ ПОИСКА:
1. Переупорядочение путем перестановки найденного элемента в начало списка.
2. Метод транспозиции.
ПОИСК ПО БИНАРНОМУ ДЕРЕВУ
Для вставки элемента в дерево сначала нужно осуществить поиск в дереве по заданному ключу. Если такой ключ имеется, то программа завершается, если нет то происходит вставка. Длительность операции поиска (число узлов, которые надо перебрать для этой цели) зависит от структуры дерева. Действительно, деревом может быть вырождено в однонаправленный список (иметь единственную ветвь) - такое дерево может возникнуть, если элементы поступали в дерево в порядке возрастания (убывания) их, ключей. В этом случае время поиска будет такое же, как и однонаправленном списке, т.е. в среднем придется перебрать N/2 элементов. Наибольший эффект использования дерева достигается в том случае, когда дерево "сбалансировано". В этом случае для поиска придется перебрать не более log2N.
ВКЛЮЧЕНИЕ ЭЛЕМЕНТА В ДЕРЕВО
Для включения новой записи в дерево, прежде всего нужно найти тот узел, к которому можно "подвесить"(присоединить) новый элемент. Алгоритм поиска нужного узла тот же самый, что и при поиске узла с заданным ключом. Этот узел будет найден в тот момент, когда в качестве очередной ссылки, определяющий ветвь дерева, в которое надо продолжить поиск, окажется ссылка NIL.
Однако, непосредственно использовать процедуру поиска нельзя, потому что по окончанию вычисления ее значение не фиксирует тот узел, из которого была выбрана ссылка NIL. Модифицируем описание процедуры поиска так, чтобы в качестве ее побочного эффекта фиксировалась ссылка на узел, в котором был найден заданный ключ (в случае успешного поиска), или ссылка на узел, после обработки которого поиск прекращен (в случае неуспешного поиска).
Удаление узла дерева не должно нарушать упорядоченность дерева. При удалении возможны следующие варианты расположения узлов:
1) найденный узел является листом - он просто удаляется (рис.1);
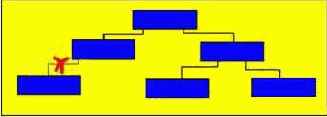
2) найденный узел имеет только сына - в этом случае сын перемещается на место удаленного отца (рис.2);
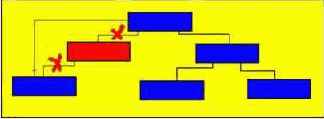
3) у удаляемого отца два сына - в этом случае основная трудность состоит в удалении отца, поскольку в удаляемую вершину входит одна стрелка, а выходит две.
В этом случае нужно найти подходящее звено поддерева, которое можно было бы вставить на место удаляемого, причем это подходящее звено должно просто перемещаться. Такое звено всегда существует:
- это самый правый элемент левого поддерева (для достижения этого звена необходимо перейти в следующую вершину по левой ветви, а затем переходить в очередные вершины только по правой ветви до тех пор, пока очередная ссылка не будет равна nil);
- это самый левый элемент правого поддерева (для достижения этого звена необходимо перейти в следующую вершину по правой ветви, а затем переходить в очередные вершины только по левой ветви до тех пор, пока очередная такая ссылка не будет равна nil).
Очевидно, что такие подходящие звенья могут иметь не более одной ветви.
При обработке данных важно знать и информационное поле данных, и размещение их в машине.
Различают внутреннюю и внешнюю сортировки:
- внутренняя сортировка - сортировка в оперативной памяти;
- внешняя сортировка - сортировка во внешней памяти.
Сортировка - это расположение данных в памяти в регулярном виде по их ключам. Регулярность рассматривают как возрастание (убывание) значения ключа от начала к концу в массиве.
Если сортируемые записи занимают большой объем памяти, то их перемещение требует больших затрат. Для того, чтобы их уменьшить, сортировку производят в таблице адресов ключей, делают перестановку указателей, т.е. сам массив не перемещается. Это метод сортировки таблицы адресов.
При сортировке могут встретиться одинаковые ключи. В этом случае при сортировке желательно расположить после сортировки одинаковые ключи в том же порядке, что и в исходном файле. Это устойчивая сортировка.
Эффективность сортировки можно рассматривать с нескольких критериев:
- время, затрачиваемое на сортировку;
- объем оперативной памяти, требуемой для сортировки;
- время, затраченное программистом на написание программы.
Выделяем первый критерий. Можно подсчитать количество сравнений при выполнении сортировки или количество перемещений.
Пусть Н = 0,01n2 + 10n - число сравнений. Если n < 1000, то второе слагаемое больше, если n > 1000, то больше первое слагаемое.
Т. е. при малых n порядок сравнения будет равен n2, при больших n порядок сравнения - n.
Порядок сравнения при сортировке лежит в пределах
от 0 (n log n) до 0 (n2); 0 (n) - идеальный случай.
Различают следующие методы сортировки:
- строгие (прямые) методы;
- улучшенные методы.
Строгие методы:
1) метод прямого включения;
2) метод прямого выбора;
3) метод прямого обмена.
Количество перемещений в этих трех методах примерно одинаково.
3.2.1 Сортировка методом прямого включения
